为什么 0.1 + 0.2 !== 0.3
整数部分的二进制表示
从十进制到二进制 :逢 2 进一
这个是非常好理解的,非常符合直觉,比如十进制的整数 13:
13(十进制) = 1×2³ + 1×2² + 0×2¹ + 1×2⁰
= 1101(二进制)₂换个视角来看:整数二进制是“2 的幂”的组合,所有整数都是用 2 的 0 次方、1次方、2次方....来组合表示的。
小数部分的二进制表示
如果还保持逢二进一的思路,到小数这就不好使了。
实际上,小数部分其实也是用 2 的幂 来表示,只是幂变成了负数,所有小数都是由 2 的 -1 次方,-2 次方....来组合表示。
| 二进制位 | 代表的权重 |
|---|---|
| 2⁻¹ | 0.5 |
| 2⁻² | 0.25 |
| 2⁻³ | 0.125 |
| 2⁻⁴ | 0.0625 |
所以:
0.625(十进制) = 0.5 + 0.125
= 1 * 2⁻¹ + 0 * 2⁻² + 1 * 2⁻³
= 0.101(10)补充:乘 2 取整法
// 计算 0.625 的二进制表示
0.625 * 2 = 1.25 --> 1
0.25 * 2 = 0.5 --> 0
0.5 * 2 = 1 --> 1
// 故
0.625(10) = 0.101(2)
// 计算 0.1 的二进制表示
0.1 × 2 = 0.2 → 0
0.2 × 2 = 0.4 → 0
0.4 × 2 = 0.8 → 0
0.8 × 2 = 1.6 → 1
0.6 × 2 = 1.2 → 1
0.2 × 2 = 0.4 → 0 // 又到了 0.2, 无限循环
// 故
0.1(10) = 0.0001100110011...(2) 无限循环这就是为什么计算机里 0.1 会是个近似值,浮点运算会有误差,毕竟用有限的位数来表示无限循环的小数。
浮点数的二进制表示
大多数现代语言的浮点数都是采用 IEEE754 标准来存储,比如 Cpp,Java,Python 等等。
在 JavaScript 里,number 就是用 IEEE 754 规定的 64 位双精度浮点数(F64)存储的
下面详细讲讲到底在内存中是怎么存储的。
存储结构
一个 F64(双精度浮点数)是 64 位,分成三段:
| 区域 | 位数 | 作用 |
|---|---|---|
| 符号位 S | 1 | 0 表示正数,1 表示负数 |
| 指数位 E | 11 | 存放“移码”指数,用来决定小数点在哪 |
| 尾数位 M | 52 | 存放有效数字(小数点左边的“1”省略存储) |
IEEE 754 计算过程,以 1.625 为例
(1) 转成二进制科学计数法
txt
1.625₁₀ = 1.101₂
// 二进制科学计数法
1.101 × 2⁰所以,符号位为 0 ,指数 0,有效数字是 1.101
注意,这里 小数点位置固定在第一个 1 后面,这是科学计数法表示的约定
(2) 指数偏移
- IEEE 754 存指数时用 偏移量(bias),F64 的 bias 是 1023。
- 指数 0 → 存储值 = 0 + 1023 = 1023
- 1023₁₀ = 01111111111₂(11 位)
(3) 有效位尾数
- 科学计数法的“1.”是默认的,不存储,只存后面的 101
- 1.101 → 尾数部分 = 1010000…(后面全补 0 到 52 位)
(4) 组合
S = 0 // 1 位符号 正数
E = 01111111111 // 11 位指数 1023
M = 101000000000...000 // 52 位尾数
// 最终内存中的 1.625 表示如下
0 01111111111 10100000000000000000000000000000000000000000000000000.1 + 0.2 !== 0.3
现在我们就可以回答这个问题了。
0.1 的二进制表示
txt
0.1 × 2 = 0.2 → 0
0.2 × 2 = 0.4 → 0
0.4 × 2 = 0.8 → 0
0.8 × 2 = 1.6 → 1
0.6 × 2 = 1.2 → 1
0.2 × 2 = 0.4 → 0 // 又到了 0.2, 无限循环
// 0 后面是 52 位
0.1(10) = 0.00011001100110011...(2)0.2 的二进制表示
可以看到,前面的循环部分就是 0.2 开始的,所以 0.2 的二进制表示也是一个无限循环小数
txt
0.2 × 2 = 0.4 → 0
0.4 × 2 = 0.8 → 0
0.8 × 2 = 1.6 → 1
0.6 × 2 = 1.2 → 1
0.2 × 2 = 0.4 → 0 // 又到了 0.2, 无限循环
// 0 后面同样 52 位
0.2(10) = 0.0011001100110011...(2)相加
txt
// 二进制相加,取个 10 位意思意思
0.0001100110 +
0.0011001100 =
0.0100110010可以看到,包不等于 0.3 的
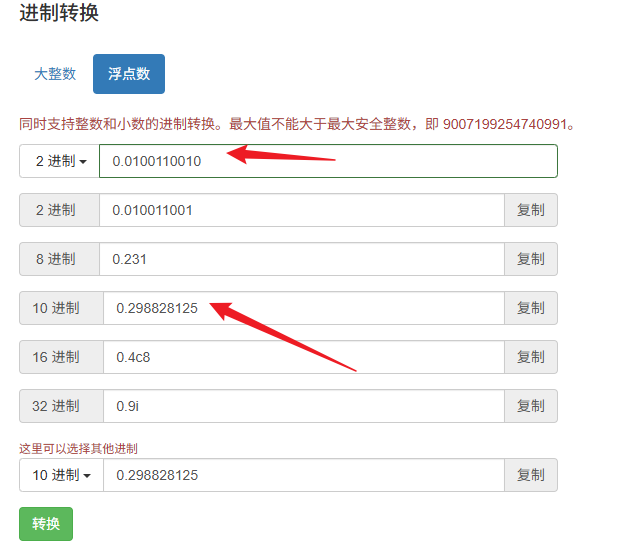
在浏览器控制台,如果我们上面的计算拉到 53 位,表现形式就一样了 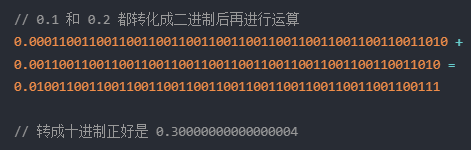
解决方案
日常开发中如何避免,如何解决这种因为浮点数精度问题导致的一些误判呢 ?
- 钱、分数、计数 → 尽量用整数存储(分、毫秒、个数)
- 判断相等 → 用
Math.abs(a - b) < Number.EPSILON - 展示结果 → 用四舍五入处理后再显示
- 高精度运算 → 用
decimal.js这类库,避免连续浮点数运算导致误差累积