Loop`s Workshop

Appearance

哈希表 ​

705. 设计哈希集合 | 706. 设计哈希映射 ​

  • 描述：实现一个类，支持add remove contains get等操作
  • 实现：
    • 用一个数组作为实际数据存储，每个元素是依然是数组(每个元素是[key, value])
    • 定一个哈希函数，把key映射到数组下标
    • 针对任何操作，就是哈希函数找到下标，然后操作数组

217. 存在重复元素 | 219. 存在重复元素 II ​

  • 描述：建立map，判断是否存在满足条件的元素即可

220. 存在重复元素 III ​

  • 描述：给nums和k，判断是否存在i和j，使得abs(nums[i] - nums[j]) <= t，且abs(i - j) <= k

  • 关键：

    • 一方面要处理滑动窗口，不断地插入和删除元素

    • 另一方面这里需要判断区间内的数是否存在，而不是前两题那种一个数是否存在，如果遍历的话，就变成O(n*k)超时

    • 所以这题用了一个比较巧的办法，通过把区间内的数放到一个桶里，这样就可以用map以O(1)的复杂度来查找判断

    • 如果valueDiff为3，那么我希望把[0,1,2]放一个桶，[3,4,5]放一个桶，[-2,-1]放一个桶,[-5,-4,-3]放一个桶，以此类推

    • 那么在查找时，就找当前数所在的桶，以及左边一个桶和右边一个桶，看是否存在满足条件的数即可

    • 桶中不需要保留所有数，只需要保留最近插入的数，否则还得遍历一次，而且窗口滑动后删除操作也麻烦

  • 实现：

    • 定义映射函数
    js
    const getID = (num, width) => {
  return Math.floor(num / width)
}
    • 核心函数
    js
    const containsNearbyAlmostDuplicate = (nums, indexDiff, valueDiff) => {
  
  const map = new Map()
  
  for(let i = 0; i < nums.length; i++) {
    
    const num = nums[i]
    const id = getID(num, valueDiff + 1)

    if(map.has(id))  //桶里已经存在数了
      return true 

    if(map.has(id - 1) && Math.abs(num - map.get(id - 1)) <= valueDiff) //左边桶存在数
      return true

    if(map.has(id + 1) && Math.abs(num - map.get(id + 1)) <= valueDiff) //右边桶存在数
      return true

    map.set(id, num)

    // 还要移除索引超了的桶
    if(i >= indexDiff) {
      map.delete(getID(nums[i - indexDiff], valueDiff + 1))
    }

  }
  return false

}

136. 只出现一次的数字 ​

  • 描述：给一个nums，其中元素要么出现一次，要么两次，找出只出现一次的数字
  • 实现：不用哈希表，从0开始，遍历字符，并异或运算，最后剩下的就是只出现一次的数字
    • 0 ^ 123 = 123
    • 123 ^ 123 = 0

349. 两个数组的交集 | 350. 两个数组的交集 II ​

  • 描述：这种写法太多了，可以排序+双指针，也可以哈希表
  • 注意：这种不要求返回结果保持原始相对顺序的，排序一下会方便很多

36. 有效的数独 ​

  • 描述：给一个9*9的数独，判断当前是否有效 (行、列、3x3小方块都不重复)
  • 实现：
    • 每一个区域是一个set，如果set中存在，则返回false
    • 所以需要 rowNum 个 set + colNum 个 set + 9个3x3小方块的set
    • 只遍历一次，对于元素[i][j]，判断rowSets[i]、colSets[j]、boxSets[i//3 + j//3]是否存在当前元素，不存在就加入

1. 两数之和 ​

  • 描述：给一个nums，和一个target，找出两个数，使得它们的和为target
  • 实现：建表的途中，找target-nums[i]是否存在

15. 三数之和 ​

  • 描述：给一个nums，找三个不等的ijk，使得nums[i] + nums[j] + nums[k] = 0
  • 实现：排序+对撞双指针。排序后，用i遍历，j=i+1,k=len-1,对撞找结果
  • 注意：恶心的地方在于去重，在找到一组结果后，i和j都需要while循环跳过重复元素

18. 四数之和 ​

  • 描述：给一个nums和target，找四个不等的ijkl，使得nums[i] + nums[j] + nums[k] + nums[l] = target
  • 实现：在三数之和基础上，再套一层循环
  • 注意：
    • 这题不能像三数之和那样剪枝
    • 这题的去重需要注意
    • 最外层循环 j 从 [0, len - 3), 考虑去重if(j>0 && nums[j] === nums[j-1]) continue
    • 第二层循环 k 从 [j + 1, len - 2), 考虑去重if(k>j+1 && nums[k] === nums[k-1]) continue
    • 内部对撞双指针 l = k + 1, r = len - 1, while去重

128. 最长连续序列 ​

  • 描述：给定nums = [100,4,200,1,3,2]，最长数字连续序列是[1,2,3,4]，返回4

  • 实现：这里写一下怎么想的

    • 首先想到的是排序，排序完就舒服了，但是题目要求O(n)
    • 想到遍历每个元素x，然后再遍历数组，找是否有x+1,有的话就继续找x+2,x+3. ..，直到找不到为止，记录长度。这显然是O(n^2)
    • 那么咱们就在查找的时候，用哈希表优化查找

  • 注意：不优化就AC不了！

    • 剪枝优化：遍历到元素x时，如果x-1存在，那么应该跳过，因为x-1的连续序列一定比x的连续序列长
    • 遍历元素优化：遍历元素时不要基于nums遍历，而是基于set中的去重后的元素来遍历

242. 有效的字母异位词 ​

基础的哈希题，先建表再查表

349. 两个数组的交集 ​

基础的哈希题，先建表再查表

1. 两数之和 ​

找数组中两个和为t的元素，那就遍历数组，遍历到x，那就看 **(t-x)**是否出现过，如果出现过那就返回x的下下标和我们存起来的t-x的下标

  1. 此处有个小坑，hash查表的结果为0时，if(0)就会无法进入循环，需要if(idx!=null) 或者用js map中的map.has("xx")

2. 四数相加 ​

还比较简单，先两层for循环，把问题转换为找（a + b）+（c + d）＝0的四元组,

  1. 注意：想想hash表的key和value应该是什么， 计数的时候不要计错了

15. 三数之和 ​

用双指针实现：通过升序排序后，用类似滑动窗口的思想查找。[current, left, right]

  1. current作为循环基数
  2. left = current + 1; right = length - 1
  3. 因为是递增的，如果sum>0则right--，如果sum<0则left++
  4. 主要恶心的是去重，需要在插入的时候添加去重逻辑，否则在结果集里去重会超时。

16. 四数之和 ​

和三数之和同理，升序排序 + 双指针(类滑动窗口)

  1. 在三数之和的外层再套一层循环
  2. 此题的target并不是恒为0， 所以不能通过第一个元素大于target就跳出， 因为即便升序排序了，负数+负数仍然会更小

41. 缺失的第一个正整数 ​

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。 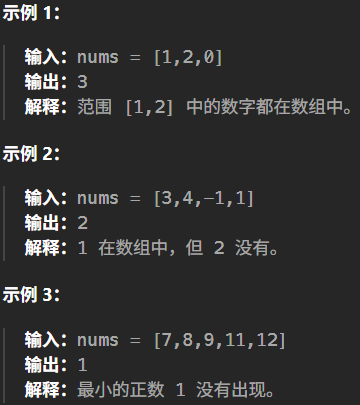首先是理解这个最小的正数如何找到 ？看到示例 3 可以明白，给一个长度为 len 的nums 数组，那就是把他和 [1,2,3, ..., len] 来比较，从左到右遍历，找到缺失的第一个正整数。

最基本的做法：把 nums 存在一个哈希表里，然后遍历 i in [1, len],一旦遇到找不到的 i ，这个 i 就是答案，非常 ez。不过不符合常数空间复杂度。

原地哈希，将数组视为哈希表。

关键是交换的时候，要一直 while 地交换，不能把合适的元素放到该在的位置就不管了

算了，不建议硬刚，有点浪费时间