动态规划 Dynamic Programming
动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。
完整掌握一道动态规划题目,需要在做题前中后思考以下问题:
- DP数组及下标的实际含义
- 递推公式
- DP数组如何初始化
- 遍历顺序要求
斐波那契数列
实现: dp[i] 即为 fib(i)dp[i] = dp[i-1] + dp[i-2]
爬楼梯
题目:求爬到第 n 层有几种方法
- 每一次可以爬两层或爬一层
实现:dp[i]为到第 i 层有几种方法dp[i] = dp[i - 1] * 1 + dp[i - 2] * 1
坑: 容易误以为dp[i - 2] 应该乘以 2,实际上应该乘以 1 dp[i-1] 中已经包含从 dp[i-2] 到 dp[i-1] 了
最小花费爬楼梯
题目:求最小花费
cost[i]是从楼梯第i个台阶向上爬需要支付的费用- 向上爬一个或者两个台阶
- 从下标为
0或下标为1的台阶开始
实现:
dp[i]为到第 i 层的最小花费dp[i] = Math.min(dp[i-2] + cost[i-2], dp[i-1] + cost[i- 1])
坑:同爬楼梯
不同路径
题目:给一个 m x n 网格,求从[0,0]到[m,n]的路径数
- 每次只能向右或向下移动
实现:
dp[i][j]为从[0,0]到[i,j]的路径数- 到达
[i,j]有两种方法,从上面,从左边 if(i>0) dp[i][j] += dp[i-1][j]if(j>0) dp[i][j] += dp[i][j-1]
不同路径II
题目:给一个 m x n 网格,求从[0,0]到[m,n]的路径数
- 每次只能向右或向下移动
- 网格中有障碍物,
grid[i][j]== 1 表示障碍物
实现:
dp[i][j]为从[0,0]到[i,j]的路径数if(grid[i][j] == 1) dp[i][j] = 0从障碍物格子到其他格子的路径数为 0- 否则
if(i>0) dp[i][j] += dp[i-1][j] if(j>0) dp[i][j] += dp[i][j-1]
整数拆分
**题目:**把一个整数拆分为几个数,使拆分乘积最大化,求最大乘积
推导:
- 最大乘积的来源?拆2个?拆多个?当然,最少是两个,在动态规划的视角里,
dp[i]就相当于把 i 拆多个得到的最大乘积。那么a * b就是拆两个a * dp[b]就是拆多个 - 两个数如何得到?对于数字n,进行一轮遍历,
i和n - i就是两个数。 - 涉及遍历,那就要维护目标值。
实现:
// dp[i] 的计算
for (let j = 0; j < i; j++) {
dp[i] = Math.max(
j * (i - j), // 两个数直接乘积
j * dp[i - j], // 多个数的乘积
dp[i]
)
}不同的二叉搜索树
题目: 求由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?
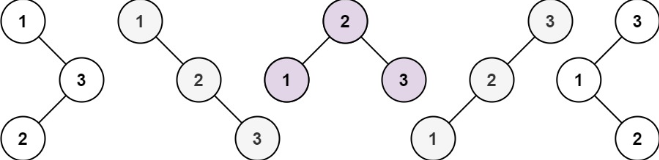
推导:
- n 个节点组成二叉搜索树和之前的
dp[n-1],dp[n-2]有关系没? - 以上面图片的为例,针对由 3 个节点组成的二叉搜索树中,通过遍历 1,2,3依次作为根节点,再考虑左右子树。
- 因为根节点固定了之后,`二叉树的种类数 = 左子树种类 * 右子树种类
- 当 1 为根节点时,左边有
1-1个节点,右边有3-1个节点,此时,左边的组合数就是dp[0]右边就是dp[2] - 以其他为根节点也同理。
实现:
dp[i]表示由 i 个节点能组成的个数- 初始化:
dp[0] = 0; `dp[1] = 1
for (let i = 2; i < n + 1; i++) {
for (let j = 0; j < i; j++) {
// 遍历节点,固定根节点为j
const leftNodeNum = j
const rightNodeNum = i - j - 1
if (leftNodeNum == 0 || rightNodeNum == 0) {
dp[i] += dp[leftNodeNum]
dp[i] += dp[rightNodeNum]
} else {
dp[i] += dp[leftNodeNum] * dp[rightNodeNum]
}
}
}买卖股票的最佳时机
题目:给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
- 只做一笔交易,一次买一次卖
- 某天买,未来卖
- 这题不是非常动态规划,有点像贪心?
实现:
- 维护一个
lowestPrice和maxProfit - 遍历
prices数组 - 在买入时,尽可能低价买入,
if (price < lowestPrice)买,更新lowestPrice - 否则只考虑卖,尽可能高价卖,
maxProfit = Math.max(maxProfit, price - lowestPrice)
买卖股票的最佳时机 ②
题目: 与上题同样只能同时持有一支股票,但是能多次操作。
DP 思路
- 能多次操作,那么每天就有两种状态,持有股票或无股票
- 今天持有可能是之前买入的继续持有,也可能是今天买入的
- 今天无股票可能是之前就一直空仓 ,也可能是今天卖了
// dp[n][2] --> dp[i][0] 表示第 i 天无股,dp[i][1]表示第 i 天持股
dp[i][0] = Math.max(
dp[i - 1][1] + prices[i], // 在 i 天卖出
dp[i - 1][0] // 在 i 天无操作,继续空仓
)
dp[i][1] = Math.max(
dp[i - 1][0] - prices[i], // 在 i 天买入
dp[i - 1][1] // 在 i 天误操作,继续持有
)注意初始化:
第一天的情况
dp[0][0] = 0 // 空仓
dp[0][1] = -price[0] // 第一天买入优化: 基于上面的推导可以看到,基本只依赖前一天的状态,所以dp数组完全可以退化为用一个状态量来保持。
贪心思路
有钱就赚
var maxProfit = function(prices) {
let ans = 0;
let n = prices.length;
for (let i = 1; i < n; ++i) {
ans += Math.max(0, prices[i] - prices[i - 1]);
}
return ans;
};买卖股票的最佳时机 3
题目:在上面两题的基础上,加上限制,最多进行两次交易,并且不能同时参与交易。 推导:
- 本质上和上题类似,上题只能操作一笔,我们用dp第二维的 0 和 1 表示
- 本题可以操作 2 笔,同时限定了必须在再次购买前出售掉之前的股票
- 故用 0,1,2,3分别表示四种状态
- 0:持有第一股
- 1:卖出第一股
- 2:持有第二股
- 3:卖出第二股
- 初始:
dp[0] = [ -prices[0],0,-prices[0],0 ]不违反题目约束 - 递推:
dp[i][0] = dp[i-1][0] 或 -prices[i]
dp[i][1] = dp[i-1][1] 或 dp[i-1][0] + prices[i]
dp[i][2] = dp[i-1][2] 或 dp[i-1][1] - prices[i]
dp[i][3] = dp[i-1][3] 或 dp[i-1][2] + prices[i]零钱兑换
题目:给定一个数组coins 表示硬币面值,求组成总金额 amount 的最少硬币数目
- 每个面值有无数个硬币
- 凑不了的话返回 -1
推导:
- 想象你在凑这个
amount,每次加入一个某面值的硬币 - 凑 n 元和我已经凑得的
n-1,n-2..n-k元有啥关系 ? - 如果我有一个面值为 k 元的硬币,那么
dp[n] = dp[n-k] + 1
实现:
dp[i]: 组成总金额 i 元需要的最小硬币数量- 目标是最小,那初始化就把
dp[i]初始化为Infinity - 初始化的
dp边界dp[0] = 0
// 对于 dp [i]
for(let c of coins){
if(i - c >= 0){
dp[i] = dp[i-c] + 1
}
}
// ...
// ...
return dp[amount] == Infinity ? -1 : dp[amount]踩坑:
- 我一开始用回溯做,然后超时了
- 凑不出的情况,可标记为
Infinity - 后来用动态规划做,
dp[i] = dp[j] + dp[i-j],还是超时了 - 最后把硬币利用好,每次我们多塞一枚硬币!
最大正方形
题目: 给定一个由'0'和'1'组成的 m * n 矩阵,求其中值为'1'的区域构成的最大正方形面积。
推导:
- 求正方形面积,就是最大正方形边长
- 单个元素 1 其实就是一个最小的正方形,如果要一个
2 * 2的正方形,对于正方形的右下角那个元素,需要满足本身值,上方值和左方值都为 1,也就是都是一个1*1正方形的右下角 - 如果要一个
3 * 3的正方形呢?对于右下角元素,它需要满足,本身是 1,左上角、左边和上边的元素都是一个2*2正方形的右下角 - 考虑定义
dp[i][j]为以[i,j]为右下角的最大正方形边长
实现:
dp[i][j]:以[i,j]为右下角的最大正方形边长- 初始化:全为 0
for(i...)
for(j...)
if(matrix[i][j] === '1'){
// 注意 Math.min()方可保证是左上方是正方形
dp[i][j] = Math.min(
dp[i - 1][j],
dp[i][j - 1],
dp[i - 1][j - 1]
) + 1
maxAns = Math.max(dp[i][j], maxAns) // 维护最大值
}最长递增子序列
题目 :子序列是相对顺序不改变的前提下部分字符构成的新串,一个字符串的最长递增子序列。 推导:需要遍历前面的元素,如果大了就 + 1,维护最大值 实现:一维 dp
for( j < i ){
if(num[i] > num[j])
dp[i] = max(dp[i], dp[j] + 1)
}最长公共子序列
题目:求两个字符串的最长公共子序列。
- 输入:text1 =
"abcde", text2 ="ace"最长公共子序列是 "ace" ,它的长度为 3 。
推导实现: dp[i][j]表示,text1的[0,i)部分 和 text2[0, j)部分的最长公共子序列。
- 当 text1[i - 1] == text2[j - 1] 时,说明两个子字符串的最后一位相等,所以最长公共子序列又增加了 1,所以 dp[i][j] = dp[i - 1][j - 1] + 1;
比如对于 ac 和 bc 而言,他们的最长公共子序列的长度等于 a 和 b 的最长公共子序列长度 0 + 1 = 1。
- 当 text1[i - 1] != text2[j - 1] 时,说明两个子字符串的最后一位不相等,那么此时的状态 dp[i][j] 应该是 dp[i - 1][j] 和 dp[i][j - 1] 的最大值。
比如对于 ace 和 bc 而言,他们的最长公共子序列的长度等于ace 和 b 的最长公共子序列长度0 与 ac 和 bc 的最长公共子序列长度1 的最大值,即 1。最长重复子数组
题目:子数组是原数组中切出来的一块,求两个整数数组的最长重复子数组。有点类似上一题,更简单一些
推导实现:
- 实现
dp[i][j]表示,num1 的[0,i)部分 和 num2[0, j)部分的最长公共子序列。 if(num1[i-1] === num2[j-1]) --> dp[i][j] = dp[i-1][j-1] + 1; 维护最大值
最小路径和
题目理解 :
- 描述:给定一个grid,求从左上角到右下角的最小路径和, 每次只能向下或者向右
- 对于格子
[i,j],到它有2条路,由左边的[i,j-1]过来,或者由上方的[i-1,j]过来 - 构成递推
dp[i,j] = min(dp[i, j-1], dp[i-1,j]) + grid[i][j]
踩坑
- 注意初始化的时候 不要写错
const dp = new Array(grid.length).fill(0).map(_ => new Array(grid[0].length).fill(Infinity))- 踩坑:使用回溯一直超时!!
最大子数组和
题目:给你一个整数数组 nums ,找出一个具有最大和的连续子数组,返回其最大和。
推导实现:
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i])- 因为只依赖前一项,还可以把 DP 数组降维为一个变量
curSum = Math.max(curSum + nums[i], nums[i])
乘积最大子数组
题目:给你一个整数数组 nums ,请找出数组中乘积最大的非空连续子数组,并返回乘积。
推导实现: - 因为有负数,所以不可以简单地 dp[i] = Math.max(dp[i - 1] * nums[i], nums[i]) - 负数 * 最大就变成了最小,负数 * 最小就变成了最大 - 需要同时维护最大乘积和最小乘积 - maxDp[i] = Math.max(maxDp[i-1] * nums[i], minDp[i-1] * nums[i], nums[i]) - minDp[i] = Math.min(maxDp[i-1] * nums[i], minDp[i-1] * nums[i], nums[i]) - ans = Math.max(ans,
分割等和子集
题目:给一个nums数组,判定该数组是否可以分为两个和相等的子集
- 题意剖析:需要恰好分为两个子集,且和相等,那这个和必然是整个数组之和的一半,那就变成了求子集里,和为sum/2的子集;也就变成了给你一堆物品和一个目标,判断能不能选出若干个物品(每个数只能用一次),使得满足目标,这就变成了01背包问题。至于另一半嘛,如果我能找出一个子集和为总和的一半,那么另一半自动就满足了。
- 最终题目:你有n个物品,这物品i的重量为
nums[i],价值为nums[j],你需要判断一个容量为sum/2的背包能装的最大价值是否是sum/2
推导和实现: - dp[i][j]:针对0-i个物品,容量为j的背包能装的最大价值 - 初始化dp[i][0]为0,dp[0][j]遍历判断能不能装第一个物品 - 典型的01背包
for (let i = 1; i < nums.length; i++) { // 遍历物品
let thingValue = nums[i]
let thingWeight = nums[i]
for (let j = 1; j < partSum + 1; j++) { // 遍历背包容量
if (j < thingWeight) { // 背包容量比物品容量还小,别考虑这个物品了
dp[i][j] = dp[i - 1][j]
continue
}
// 有可能塞进来
const v1 = dp[i - 1][j] // 不塞
const v2 = dp[i - 1][j - thingWeight] + thingValue // 塞
dp[i][j] = Math.max(v1, v2)
}
}最后一块石头的重量
题目:给Stones,其中石头两两可以攻击破坏,求最终剩余的石头最小重量
- 题意剖析:两两可破坏,求最终剩最小,那就变成了尽可能分为两组大小相等的石头,这就变成了上一题-求和相等的子集,变成了找重量为sum/2的包的价值
- 最终题目:你有n个物品,每个物品价值为stones[i],重量为stones[i],求重量为sum/2的包的价值和sum/2之间的diff
编辑距离
题目:把一个字符串编辑为另一个字符串的最小操作次数,可以替换、删除、插入
理解和推导:
dp[i][j] 将 word1[0,i) 变到 word2[0,j)需要几步
已知 dp[0][0] = 0; 那么:
- 插入 dp[0][1] = 1;
- 删除 dp[1][0] = 1;
- 替换 dp[1][1] = 0 or 1
对于替换的理解,已知dp[i-1][j-1], 现在 word1[i] !== word2[j], 那么把 word1[i] 替换为word2[j]就行了,也是一次操作
===========================================================
综上:
word1[i] === word2[j] ? dp[i][j] = dp[i-1][j-1]
word1[i] !== word2[j] ?
dp[i][j] = 【dp[i-1][j] + 1 】 or
【dp[i+1][j] + 1 】 or
【dp[i-1][j-1] + 1 】推导和实现:
var minDistance = function (word1, word2) {
const dp = new Array(word1.length + 1).fill(0).map(_ => new Array(word2.length + 1).fill(Infinity))
for (let i = 0; i < word1.length + 1; i++) {
dp[i][0] = i // 删除 i 次
}
for (let j = 0; j < word2.length + 1; j++) {
dp[0][j] = j // 插入 j 次
}
for (let i = 1; i < word1.length + 1; i++) {
for (let j = 1; j < word2.length + 1; j++) {
if (word1[i - 1] === word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1]
} else {
dp[i][j] = Math.min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]) + 1
}
}
}
return dp[word1.length][word2.length]
};最长有效括号
题目:
- 描述:给一个只包含
(和)的字符串,求正确且连续的最长子串长度 - 比如:s = ")()())" 输出 4 因为最长有效括号子串是 "()()"
注意:
()(()()')'这种情况,新加入的括号链接了两个串!
实现:
dp[i]表示从0到以索引 i 结尾的子串的有效括号子串长度。- 遍历字符c,索引 i ,如果遇到
(,直接跳过,dp[i] = 0 - 如果遇到
), 检查前一个字符s[i-1],如果是(,也就意味着此时字符串形如...(),刚好可以凑上一对,再加之前面的有效长度,dp[i] = dp[i-2] + 2 - 如果前一个字符也是
),那就要考虑这么一种情况: 当()(()再遇到一个)时,就实现了有效字符串的合并。 - 所以,开始检查这个可能作为连接中心的字符是否为左括号
s[i-dp[i-1]-1] === '(' - 如果是,那就进行长度合并
dp[i] = dp[i-1] + dp[i-dp[i-1]-2] + 2
var longestValidParentheses = function (s) {
// dp + stack
const dp = new Array(s.length).fill(0);
dp[0] = 0;
let ans = 0;
for (let i = 1; i < s.length; i++) {
if (s[i] == "(") {
dp[i] = 0;
continue;
}
// dp[i] == ')'
if (s[i - 1] == "(") {
// 字符串为 ....()
// 刚好可以凑一对, 加上前边的
dp[i] = i >= 2 ? dp[i - 2] + 2 : 2;
}
if (s[i - 1] == ")") {
// 字符串为 ....))
// 如果 i-1 组成的有效括号的再前一个为“(”, 那刚好可以再和这个新遇到的")" 匹配上
if (i - dp[i - 1] - 1 >= 0 && s[i - dp[i - 1] - 1] === "(") {
// 字符串为 ...((...)),中间是有效的
if (i - dp[i - 1] - 2 >= 0) {
// 此时,新遇到的 ) 使得两个有效长度的括号合并了
// 有效长度应该是 dp[i - dp[i - 1] - 2] + dp[i-1] + 2
dp[i] = dp[i - dp[i - 1] - 2] + dp[i - 1] + 2;
} else {
// 此时,没有前面的有效括号,上一个有效括号的长度 + 2
dp[i] = dp[i - 1] + 2;
}
}
}
ans = Math.max(ans, dp[i]);
}
return ans;
};单词拆分
 这题我一开始用回溯
这题我一开始用回溯
从 i 开始
for j in range [i, len-1]
sub = s.slice(i,j+1)
if(dict.has(sub)){
// 能找到匹配的单词的话,就继续从j+1往下go
let oldCurStr = curStr
curStr = oldCurStr + sub
backTrack(j + 1)
curStr = oldCurStr // 回溯,因为会有sand, and, cat, cats这些情况
}逻辑上是没毛病的,但是超时了。
改为DP
dp[i]: 前 i 个字符能否被凑成,我们的目标变成了求 dp[n]
dp[0] = 0
dp[i] = for j in [0, i] { dp[j] && dict.has(s.slice(j,i)) }
有点零钱兑换那意思5. 最长回文子串
描述:给定一个字符串,求其中的最长回文子串
注意:这题是子串问题,要保持原顺序,找到原始串中满足条件的一个子串
思路:
- 动态规划法,
dp[i][j]表示[i,j]是否是回文串,存个 boolean 即可,dp[i][j] = dp[i+1][j-1] && s[i] === s[j],维护最大值
- 动态规划法,
实现:
dp[i][j]表示[i,j]是否是回文串,故这个二维数组只有右上部分的值是有效的,初始化只处理dp[i][i]dp[i][j]依赖于dp[i+1][j-1],所以i从大到小遍历,j从i+1到大遍历- 只有当
j>i+1时,才需要判断dp[i][j],否则dp[i][j] = dp[i] === dp[j]
还有一个中心探测法,更高效,遍历每个元素作为中心,从中心往左右双指针探测。
516. 最长回文子序列
子序列:是可以jump的,保留相对顺序即可。  同样的,核心是 回文串去除首尾仍然是回文串
同样的,核心是 回文串去除首尾仍然是回文串dp[i][j] = dp[i + 1][j - 1] + 2
含义: dp[i][j]: s[i,j]这部分的最长回文子序列
初始化:只有 j >= i 的部分有意义,dp[i][i] = 1
遍历:i依赖于i+1,所以从大到小,j依赖于j-1,所以从小到大
递推:
i==j --> dp[i][j] = 1
j==i+1 --> if si = sj : dp[i][j] = 2
else : dp[i][j] = 1
j> i+1 --> if si = sj : dp[i][j] = dp[i + 1][j - 1] + 2
else : dp[i][j] = max(dp[i+1][j],dp[i][j-1])