Loop`s Workshop

Appearance

回溯 ​

回溯回溯本质上是也是一种暴力递归，但总能解决固定几层循环解决不了的问题。 通过在每一步尝试所有可能的选择，并记录路径。找到一条路径or遇到不可行路径时，回退到上一步重新选择

总结来说，回溯算法适合那些需要穷举所有可能性, 层次深度不确定的场景，典型的场景有：

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 排列问题：N个数按一定规则全排列，有几种排列方式(强调顺序)
  • 棋盘问题：N皇后，解数独等等
js
// 回溯模板
function backtrack(路径, 选择列表) {
    if (满足结束条件) {
        result.push(路径)
        return
    }
    for (选择 in 选择列表) {
        做选择，更新路径
        backtrack(路径, 选择列表)
        撤销选择，恢复路径
    }
}

组合问题 ​

还比较清晰，注意startIndex的取值，注意选择列表

分割问题 ​

注意切割的实现

![pic](./image/131. 分割回文串.jpg)

js
    function backTracing(startIndex) {
        if (startIndex == originString.length) {
            result.push(path.slice())
            return
        }

        for (let i = startIndex; i < originString.length; i++) {

            const splitSubStr = originString.slice(startIndex, i + 1) // 切割startIndex到i的字符串
            if (isValid(splitSubStr)) {
                path.push(splitSubStr)
                backTracing(i + 1)
                path.pop()
            }
        }
    }

子集问题 ​

  • leetcode 78

组合问题是只收集遍历树的叶子，子集问题是全都收集，所以终止条件的结果path收集那部分小有区别

  • leetcode 90 子集-ii
  • leetcode 491 非递减子序列

核心是关于去重的实现，主要包括树枝去重和树层去重, “树层去重看 used，树枝去重不管 used。”

js
if (i > 0 && nums[i] === nums[i - 1]) continue

这种情况叫做 “树层剪枝”，也就是无论前面那个数有没有被用过，只要值一样就跳过。
这会导致什么呢？——错杀！

举个例子，假设你正在构造 [1,1,2] 的排列：

  • 当你在第2层递归选择了第二个 1 时，如果前面的 1 是已经被使用的（路径的一部分），但你因为两个 1 相同就跳过了，那就永远也构造不出像 [1,1,2] 这样的排列了。会漏掉一些合法的排列。
js
if (i > 0 && nums[i] === nums[i - 1] && used[i - 1]) continue

只有当前面那个相同的数已经被用过了（也就是它已经在当前路径里了），才跳过当前这个重复的选择。

这种写法叫做 “树枝剪枝”，它只会阻止那些会造成重复排列的分支，不会影响到正常构造重复元素的情况。

排列问题 ​

排列通常是考虑顺序的，在数层|树枝的剪枝上也更为重要

棋盘 ​

  • N皇后，本质上还是一个套路，只是把皇后落子的判断按题意完成即可。
js
var solveNQueens = function (n) {

    const res = []
    const path = []

    function isValid(_path, _rowIndex, _Qindex) {
        // 判断当前落子是否合理
        if (_path.length === 0) return true

        for (let row = 0; row < _path.length; row++) {

            // 同一列则kill, 同一行不考虑，我们本身就是逐行落子的
            if (_path[row] === _Qindex) return false

            // 斜线kill， 斜线体现为两个Q的deltaRow和deltaCol相同
            let deltaRow = Math.abs(_rowIndex - row)
            let deltaCol = Math.abs(_Qindex - _path[row])
            if (deltaRow === deltaCol) return false

        }

        return true
    }

    function backTrack(rowIndex) {

        if (rowIndex === n) {
            // n行都已经排好了，记录
            res.push(path.slice())
        }

        // 遍历这一行的n列，逐个试探落子
        for (let i = 0; i < n; i++) {

            if (isValid(path, rowIndex, i)) {

                path.push(i)
                backTrack(rowIndex + 1)
                path.pop()
            }
        }
    }

    backTrack(0)

    // 将结果处理为题目要求的 ...Q...
    let result = []
    for (let oneRes of res) {

        let oneResult = []
        for (let row = 0; row < n; row++) {

            const Qindex = oneRes[row]
            const thisRow = new Array(n).fill('.')
            thisRow[Qindex] = 'Q'

            oneResult.push(thisRow.join(''))
        }

        result.push(oneResult)
    }

    return result
};

题目 ​

全排列 ​

全排列主要是在回溯过程中，需要记录有哪些数字可用

方法一：使用 filter 过滤 availableNums , 效率低

js
 const backTrack = (availableNums) => {
        if (cur.length === nums.length) {
            res.push(cur.slice())
            return
        }
        for (const num of availableNums) {
            cur.push(num)
            backTrack(availableNums.filter(n => n != num))
            cur.pop()
        }
    }

方法二：用一个全局的 visited 数组来记录，同样参与回溯

93. 复原 IP ​

题目如下：给字符串，输出所有可能的 ip 地址

条件：

  • 每个部分是 1 - 3 个字符， 区间是 [0, 255]
  • 共四个部分
  • '0' 是 ok 的，但 ’00‘ ’05‘ 是不合法的
  • 要把字符用完！

思路：回溯 + 具体条件判定 自然是带着 startId 的回溯，每次循环内不用全部遍历，遍历 [startId, startId + 2 ] 即可。

js
var restoreIpAddresses = function (s) {
	res = []
	path = []
	
	function bTrace(startId){
		// 四个部分
		if(path.length > 4) return
		// 要把 s.length 个字符用完 
		if(path.length === 4 && startId == s.length){
			res.push(path.join('.'))
			return			
		}
		// 循环回溯， 1-3 个字符
		for(let i = startId; i< s.length && i < startId + 3; i++){
			const substr = s.slice(startId, i + 1)
			// 0 - 255 判断
			if(parseInt(substr) > 255) 
				continue
			// 前导 0 判断
			if(substr.length > 1 && substr[0] === '0')
				continue
			// 回溯
			path.push(substr)
			bTrace(i+1)
			path.pop()
		}
	}
	bTrace(0)
	return res
}

39. 组合总和 ​

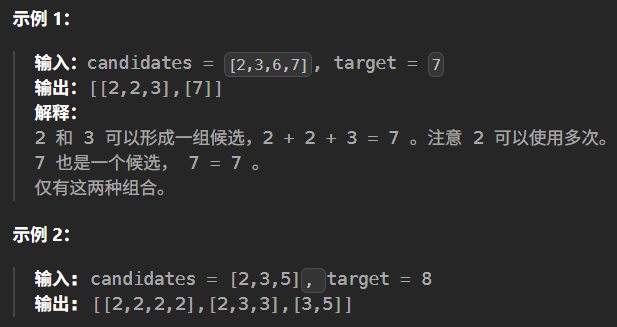数字可以用多次，去重问题。

解决 223 和 232 的问题即可

  • 每次给一个startId
  • for i in range (startId, len)
    • backTrack(i) // 不是 i + 1哈，因为数字可以重复用

40. 组合总和 2 ​

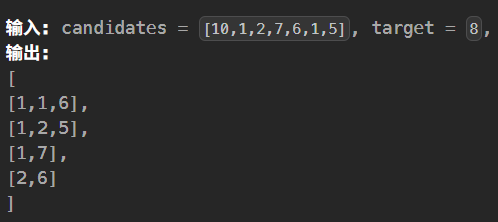比较恶心的是 [1,2,5] 和 [2,1,5] 被视为同一个，需要去重。

去重：通过给 candidates 排序，在 for 的时候滑动即可。

这里小结一下回溯里面几种控制流：

  • 排序 + for 滑动
  • visited 访问标记
  • startId 控制方向